開管の固有振動数

概要

両端が開いた管を開管という。例えばリコーダーは、実は下の部分に穴が空いているので、開管の一種である。片方が閉じた管を閉管といい、そちらについては閉管の辞書で学ぼう。

弦の固有振動のときと同じように、気柱である開管に、両端が腹になる定常波を作ったときの、振動数について考えよう。

※開管では両端が開いているので、外側の空気と接している部分の空気が動きやすく、定常波の腹になる（現実には、両端よりもう少し外側の部分が腹になる。後ほど補足）。

このような定常波が作られるような波の振動数は、どんな値でもいいわけではなく、 を開管の長さ、 を音の速さとして、次のようなとびとびの形となる。

これを、開管の固有振動数という。

弦の場合と異なり、波を伝える媒質は空気となるので、音速 を用いる点に注意。

導出

ここでは上の、

を導いてみよう。まず、音の速さは一定なので、波の基本式

により、波長 が大きいほど振動数 は小さくなることがわかる。

では、一番小さい固有振動数はどのような場合かというと、波長が一番長いときで、こんな振動になるはず。

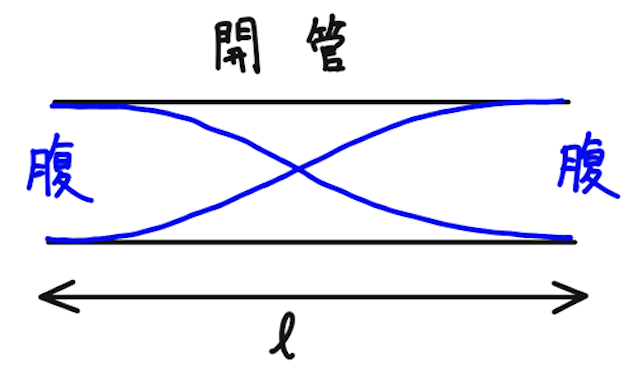
このとき、左右に折り返すとわかる通り、波長は になる。

よって、このときの固有振動数は、

となり、この振動を、最小の固有振動数を持つ振動という意味で、基本振動という。

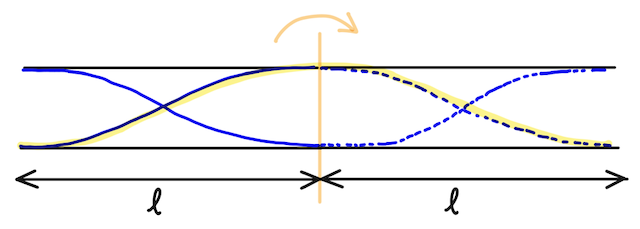
その次に大きい固有振動数のときは、少し考えてみると、波長は になる。

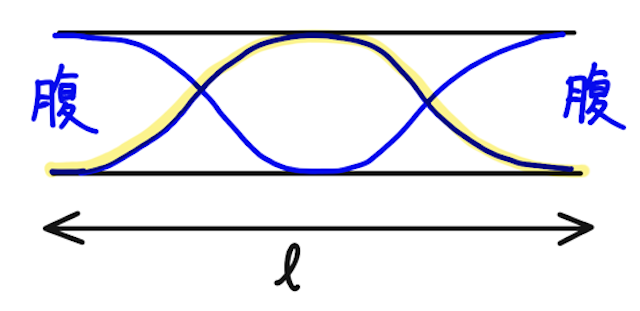
よって、このときの固有振動数は、

となり、基本振動のときの振動数の 倍となる。なので、この振動を 倍振動という。以下同様に、 倍振動、... というように増えていく。

では、 として、一般的な 倍振動の固有振動数を求めよう。

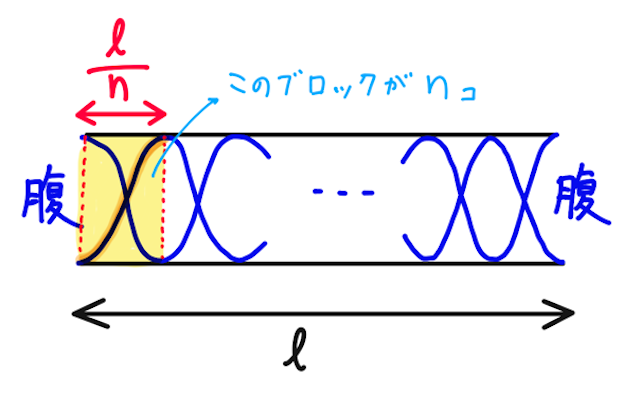
このとき、上の黄色のブロックが 個できるので、 つのブロックの長さが となり、これが半波長 と等しいので、

と求められる。よって、振動数は、

と求められる。

補足

現実には、管の両端ピッタリが定常波の腹になるわけではなく、ちょびっとはみ出たところが腹になる。例えば基本振動を考えると、

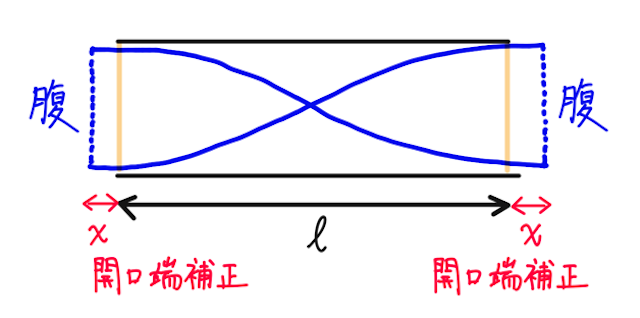
こんな感じで、管の両端から少し離れたところに腹がくることになり、なので、波長を求める上で、管の長さに加えて少し補正をしてあげる必要がある。これを開口端補正という。

両方の補正分をそれぞれ とすると、基本振動のときの波長は、 となるので、振動数は、

となる。