第二宇宙速度

概要

地球の表面から何かを投げるシリーズの第二弾。第一宇宙速度よりも物体の速さが大きくなると、物体の軌道は楕円（だ円）を描くようになる。さらに初速度を大きくしていくと、物体は無限遠に飛んでいくことになる（双曲線軌道に変わる）。

無限遠に飛んでいくための速さの最小値（ギリギリ飛んでいく速さ）のことを、第二宇宙速度という。

この速度を理論的に求めてみよう。地球の半径を 、重力加速度を とすると、第二宇宙速度 は

で求められる。よく名前に引っ張られて としてしまいがちなので注意しよう。

導出

地球の質量を 、物体の質量を 、 地球の半径を 、地表での重力加速度を とする。この物体は万有引力のみを受けて運動する。

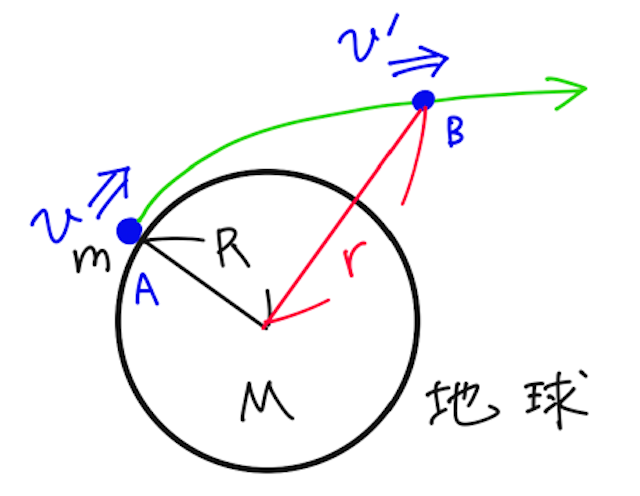
円軌道ではないので運動方程式を考えるのは厳しいので、2時点間のエネルギー保存則を考える。万有引力による位置エネルギーの基準点を無限遠とすると、打ち上げ時点と、地球からの距離が となった時点とのエネルギー保存則の式は、

となる。（運動エネルギーと、万有引力による位置エネルギーの和が保存する）

この物体が無限遠まで飛んでいくための条件は、 とした時に、 が存在することである。

とすると、

このとき、 が存在するための条件は、

となるので、無限遠に飛んでいくための速さの最小値である第二宇宙速度 は、

とわかる。

ここで、重力加速度と万有引力定数の間の関係式より、

が成り立つ。（上の辞書では で考えていたが、今回 は地表での重力加速度なので、 で考えてOK）

よって、第二宇宙速度は

と求められる。

補足

数値で求めてみよう。重力加速度と地球の半径はそれぞれ

なので、第二宇宙速度は

となる。どれくらいの速さかというと、新幹線の最高スピードの120倍ほど速い。

「ギリギリ飛んでいく」というのがとてもイメージしづらいが、実は物体の初速度を上げていくと、楕円軌道から双曲線軌道に切り替わる際に、物体は放物線軌道を描く。 この放物線軌道を描くための速さが、第二宇宙速度というイメージ。

地上から打ち上げた物体が、地球の周りを回り続けるために必要な最小の初速度である 第一宇宙速度 もよく問われるので、違いがわかる人になろう。

ちなみに、あまり出てこないが第三宇宙速度もあり、これは太陽系を抜け出して飛んでいくのに必要な最小の初速度を意味する。