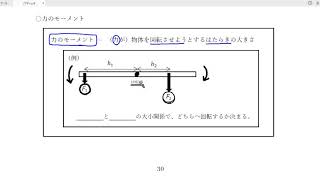
剛体のつり合い

概要

大きさのない質点についての運動を考えるときは、その質点が移動していく運動（並進運動という）だけを考えればよかった。その際に、加速度運動をしない条件として、合力が という力のつり合いというものを考えた。

しかし大きさを考える必要のある 「剛体」 についての運動を考える場合には、並進運動に加えて、物体の回転運動も考えていく必要がある。

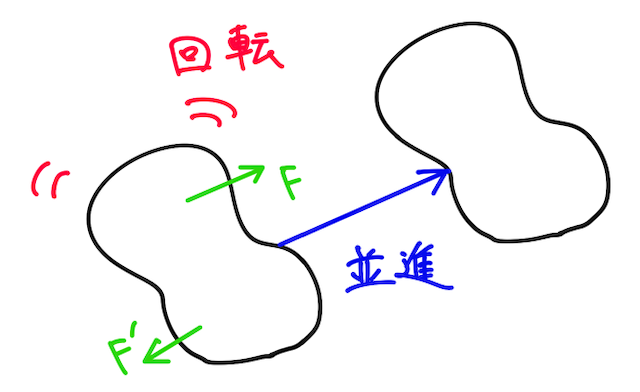
そこで剛体の場合には、剛体の重心が加速度運動することなく、かつ回転しないとき、「剛体にはたらく力がつり合っている」 という。

つまり、剛体のつり合いの条件は2つあり、

• 合力が であること
• 力のモーメントが であること

となる。力のモーメントの辞書はこちらから（ある点のまわりで、回転するかどうかを考えるための値だったことを復習しよう）。

ここで、剛体が回転しないためには、どの点のまわりにも回転しない、つまりどの点のまわりのモーメントも0になることが必要になってくる。ただ実は、剛体にはたらく合力が であるとき、ある一点のまわりのモーメントが0であれば、任意の点のまわりのモーメントが0になる、という性質が成り立つ。（証明はここでは割愛）

なので、剛体のつり合いの条件は、

• 合力が であること
• ある点のまわりの力のモーメントが であること

となり、これが剛体が加速度運動せず、回転しない条件となる。合力の条件はベクトルの式であることに注意しよう（↓ の解き方も参照）。

解き方

「結局どうやって解いたらええねん！」となるので、剛体のつり合いの解き方をまとめると、実践的には

• 成分ごとの力のつり合いの式（平面だと つ）
• 適当な点まわりの力のモーメントが （力がたくさん集まっている点を選ぶとラク）

の計3つの式を立てれば基本的にはなんでも解ける。

下の例で確認しよう。

例

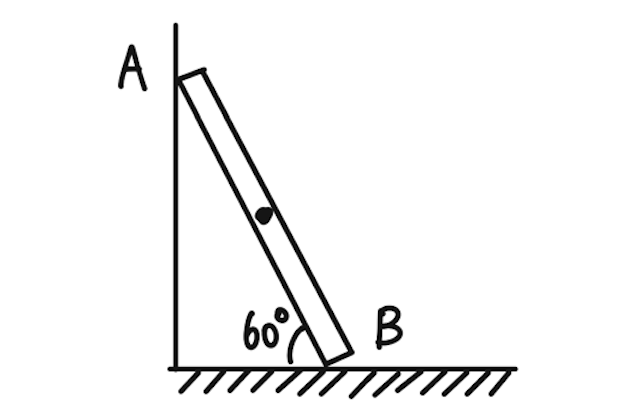
【問】重力 の一様な棒を、水平で粗い床と60°の角をなすように立てかける。鉛直な壁は滑らかとする。このとき、

• 棒の上端Aが壁から受ける垂直抗力の大きさ
• 下端Bが床から受ける垂直抗力の大きさ
• 下端Bが床から受ける摩擦力の大きさ

をそれぞれ求めよ。

【答】

はたらく力は以下の通り。

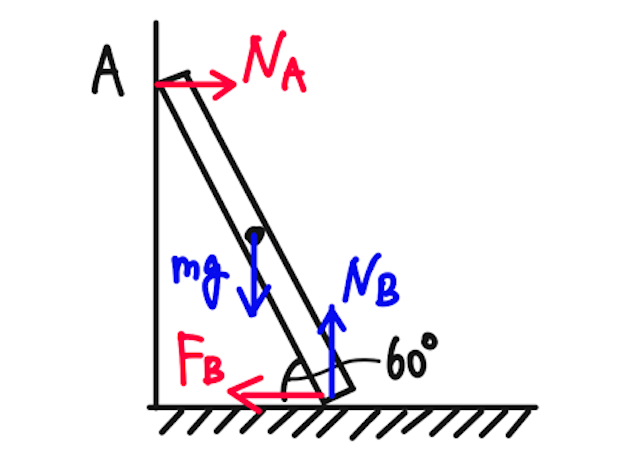
まず、水平方向の力のつり合い（合力が0）より、

鉛直方向の力のつり合いより、

そして、棒の長さを とおくと、棒の下端Bまわりの力のモーメントのつり合いより、

となる。整理すると、結局 は消去できて、

を得る。

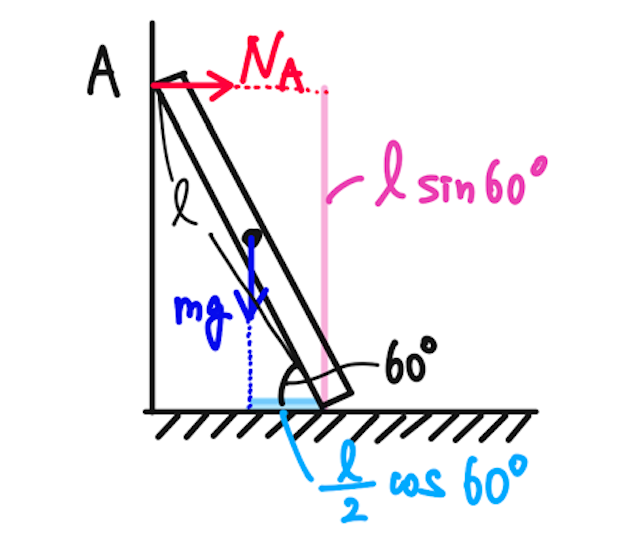
大事なのは、どの点のまわりのモーメントを考えると楽かというところ。力がたくさん集まっているところを中心にすると、考える力のモーメントが減って楽になることが多い。

あとは(1)〜(3)を解けばよく、

(3)より、

(2)より、

(1)より、

と求められる。

この壁に立てかける棒の問題は、剛体の分野で定期テストなどでよく登場するので、まとめて演習しておこう。okkeの関連動画はこちらから。