曲線の長さ

概要

数学3の積分の最後の方に登場するので、無視されがちな公式であるものの、入試で登場することもあるので、必要になれば思い出せるようになっておこう。

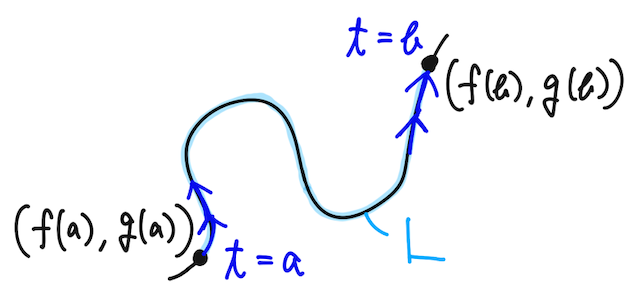
平面上の曲線が、媒介変数（パラメータ） を用いて

と表されるとき、この曲線の長さ は

で表される。

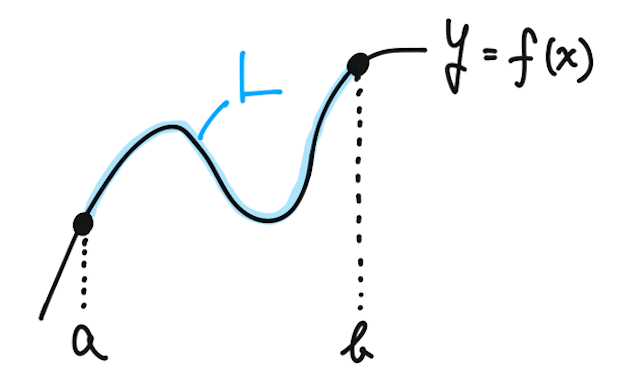
また、曲線の方程式が

の形である場合には、先ほどの式で

とおけばよく、

なので、 に代入すると、曲線の長さ は

で表されることがわかる。

媒介変数表示のときは上の の式、 の形のときは下の の式を使うと頭を整理しておこう！

簡単な証明

ここでは が成り立つ理由について、教科書的な説明で雰囲気を理解しておこう。

動画で理解したい方は、

• 簡潔に学びたい方は高瀬先生の動画
• 詳しめに学びたい方はAKITOさんの動画

がオススメ！

平面上の曲線が、媒介変数（パラメータ） を用いて

と表されるとき、始点 から点 までの曲線の距離を とおく。

このとき、曲線の長さ は

で求められるので、これを求めていこう。

を に増やしたときに、 がそれぞれ になるとし、点 を次のようにおく。

が極めて小さい正の値のとき、 の増分

は、線分 の長さにほぼ等しい。

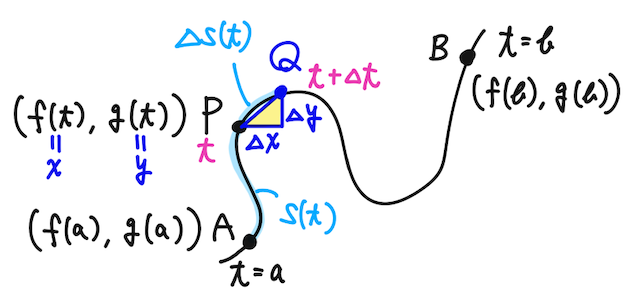
よって、

を得る。両辺 で割ると、

となり、ここで とすると、

よって、これを で積分すると、

と求められる。

例

【問1】

で表される曲線の の部分の長さ を求めよ。

【答1】

より、求める長さ は、

と求められる（ を用いた）。実は問題文の媒介変数表示は、半径1の円を表しており、求める長さは、上半分の円周の長さとなるので、

と求めることもできる。（円の媒介変数表示の辞書はこちら）

【問2】

で表される曲線の の部分の長さ を求めよ。

【答2】指数関数の導関数を考えると、

より、求める長さ は、

と求められる。（ の形で方程式が与えられていたので、 を用いた）

ちなみに、今回の

という曲線には、カテナリー（懸垂線） という名前がついていて、糸などを水平に張ったときに自分の重みでたわんだ曲線は、このタイプの式で表される。

補足

平面上の曲線が極座標で表示されている場合がたまに登場し、その場合の曲線の長さの公式も存在するので紹介する。曲線 の長さは、

で表される。導出は林俊介さんの動画で確認しよう。

問題で出た場合には、直交座標での媒介変数表示に変換し、上の を使って長さを求めることもできるので、この公式は必須知識ではないものの、知っていると計算がラクになることが多い。

入試問題としては、例えば2009年に京大で出題されている。同じく林俊介さんが、直交座標でも極座標でも解説されているので、動画で確認しよう。