弦の固有振動数

概要

両端を固定した弦を弾くと、うまく弾くことで両端を節とする定常波を作り出すことができる。

これは、弦を左右に伝わっていった横波が、固定端（辞書作成中）である両端で反射し、反射波と重なり合っていくことで作られる。

このような定常波が作られるような波の振動数は、どんな値でもいいわけではなく、 を弦の長さ、 を弦を伝わる波の速さとして、次のようなとびとびの形となる。

これを、弦の固有振動数という。

これは、弦の長さや、下で見るように線密度などで決まる値であり、弦それぞれに固有の値、というイメージ。下のチャプターで確認しよう。

また、弦を伝わる波の速さは、その弦の張力を （断面積と間違いやすいので注意！）、線密度を とすると、実は

と表される。綿密度とは、弦の単位長さあたりの質量のことであり、質量を 、長さを とすると、

で求めることができる。なので、線密度の単位は となる。

この波の速さを用いると、弦の固有振動数は、

と表すことができる。

導出

ここではまず、

を導いてみよう。まず、弦を伝わる波の速さは、弦によって決まったものであるので、波の基本式

により、波長 が大きいほど振動数 は小さくなることがわかる。

では、一番小さい固有振動数はどのような場合かというと、波長が一番長いときで、こんな振動になるはず。

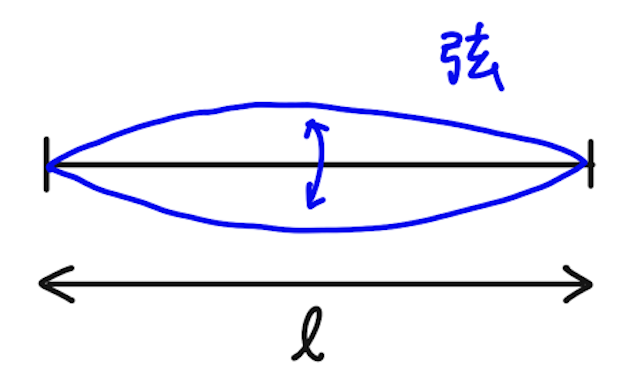
このとき、左右に折り返すとわかる通り、波長は になる。

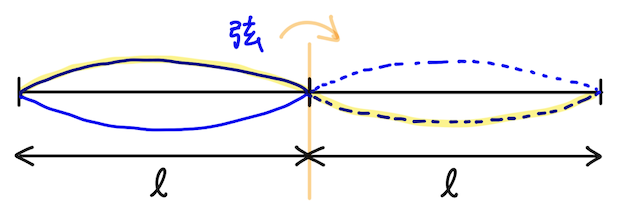
よって、このときの固有振動数は、

となり、この振動を、最小の固有振動数を持つ振動という意味で、基本振動という。

その次に大きい固有振動数のときは、少し考えてみると、波長は になる。

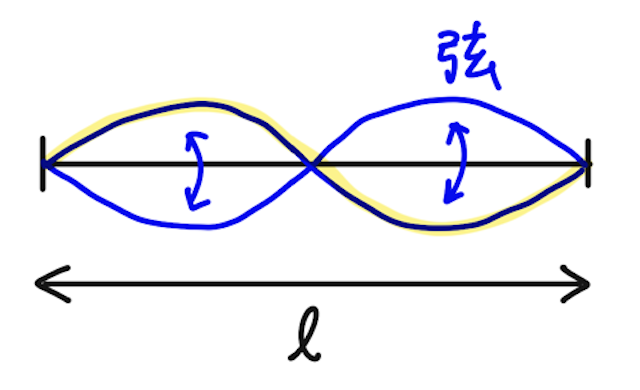
よって、このときの固有振動数は、

となり、基本振動のときの振動数の 倍となる。なので、この振動を 倍振動という。以下同様に、 倍振動、... というように増えていく。

では、 として、一般的な 倍振動の固有振動数を求めよう。

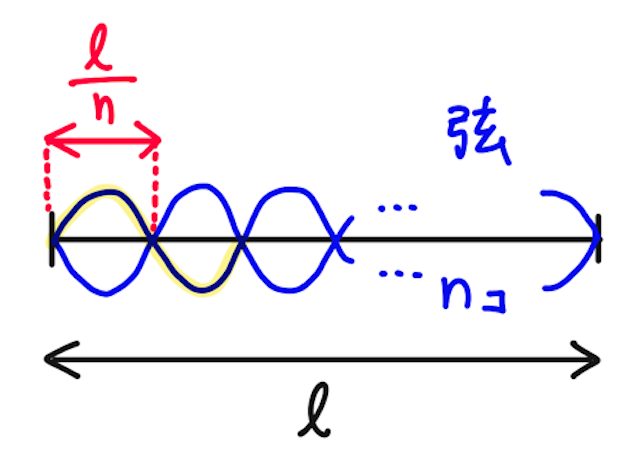
このとき、膨らみが 個できるので、 つの膨らみの長さが となり、これが半波長 と等しいので、

と求められる。よって、振動数は、

と求められる。

弦を伝わる波の速さ

この式は忘れやすいので、ここでは証明ではなく、思い出し方を紹介してみる。（証明は発展的な事項で、結構大変。興味がある方は、この長旅Pさんの動画で学ぼう）

それは単位に注目することで、弦を伝わる波の速さの式

の両辺に注目すると、左辺の単位は であり、右辺の単位は、

であるが、運動方程式を思い出すと、 なので、

となり、左辺と一致する。この方法で、ルートのつけ忘れなどを防げる！

補足

開管の固有振動数や閉管の固有振動数と違って、 は音速ではなく、弦を伝わる波の速さである点に注意しよう。

また、おんさ（音叉）に弦を取り付けてみる。おんさは振幅が小さく、近似的に固定端と見なすことができる。

実はこのとき、おんさとの取り付け方によって弦に伝わる振動数が変わるので要注意。

下のような向きに弦を取り付けると、おんさの振動数と弦に伝わる振動数は同じとなる。

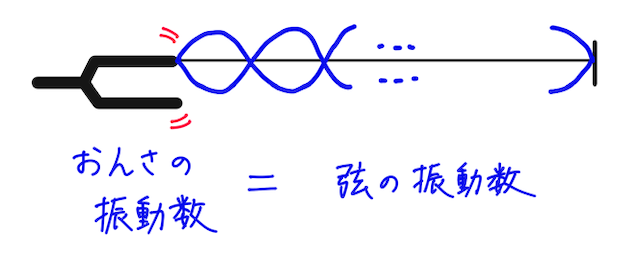
一方で、下のような向きに弦を取り付けると、おんさが 回振動する間に、弦は 回振動することになり、弦の振動の振動数は、おんさの振動数の半分になる点に注意！たまにひっかけ問題として出てくる。

ではなぜおんさが 回振動する間に、弦は 回振動するのか、絵で見た方がわかりやすいので、下で確認しよう。

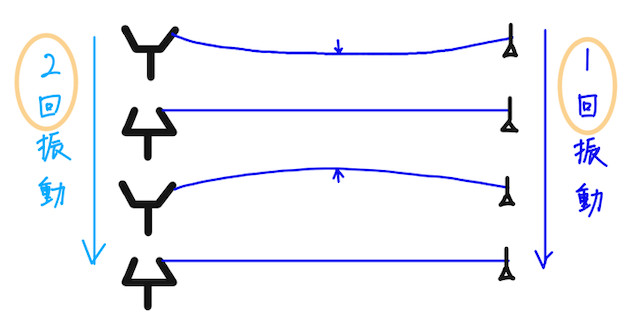
※実際はおんさはこんなに大きく開いたり閉じたりしない。

つまり、おんさが開くときに、弦が上にたゆむときと下にたゆむときの パターンがあり、それを繰り返すことになる。