うなりの振動数

概要

振動数がわずかに異なる2つのおんさを同時に鳴らすと、ウォーンウォーンと、音が周期的に大きくなったり小さくなったりする現象を起こすことができる。この現象をうなりという。

ドップラー効果と違って、あまり日常で接する機会がないので、覚えては忘れ去られる現象の一つ。

そのウォーンウォーンが1秒間に何回起こるかが、うなりの振動数 であり、それは2つのおんさの振動数の差の絶対値で求められる。

これは公式を使えるようになっておけば十分だが、興味のある人は、下の導出まで確認しよう。

イメージ

振動数 の音波が重なり合う場合、2つの音波の位相が逆位相になった時刻では弱め合うことになり、合成波の振幅は0になる。

そして、次に逆位相になるまでの時間 の間に、下の図の通り、合成波は弱め合い → 強め合い → 弱め合いという流れになり、この時間 でうなりが1回生じる（ウォーンが1回起こる）。（振動数が異なるので、必ずどこかで強め合う）

よって、うなりの周期は となる。

この時間 の間で何が起こっているかというと、下の図の通り、音波の山の数が1つだけ違っていることになる。

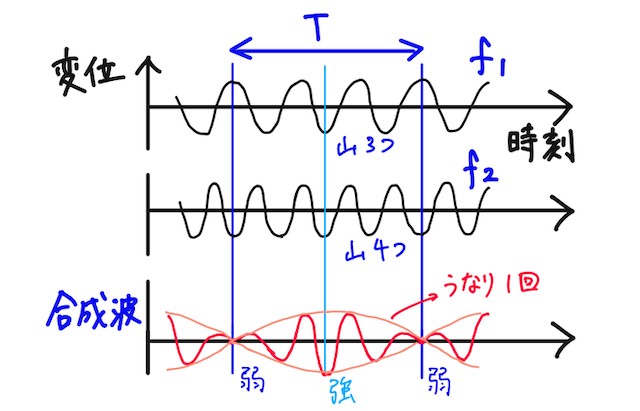
つまり、

となる。よって、うなりの振動数は、波の基本式から、

と求められる。

動画で学びたい人は、物理屋チャンネルnaoさんのこの動画がオススメです！

波の式による説明（発展）

波の式を用いて、数式で考えることもできる。2つの波の での変位を、

とおく。このとき、 での合成波の変位 は、和積公式を用いると、

となる。ここで、 に比べて、 はとても小さいので、 の中の位相の周期のような時間では、 の中の位相はほとんど変化しない。よって、この式を、

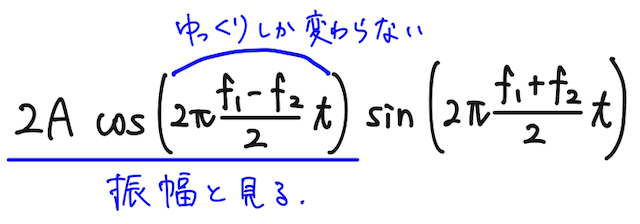
と見ることにすると、振幅の2乗が音の大きさを決めるので、

の周期を求めれば、それがうなりの周期となる。

半角の公式から、

であるので、うなりの周期は

であることが示される。（この時間で位相が 変化することを確認しよう）

動画で学びたい人は、ヨビノリさんのこの動画がオススメ！

補足

振動数が 「わずかに」 異なるというのが引っかかる方もいるかもしれない。じゃあだいぶ違う時はどうなるのか気になるところだが、その場合は別の音が2つ聞こえることになる。

例えば、ピアノのドの音と、めっちゃドに近い音を同時に鳴らすとうなりが起こるが、ドの音と同時に、振動数のだいぶ違うミの音を鳴らすと、それはもはや「ド」と「ミ」の音として和音が聞こえるはず。（これもうなりが起きたら、曲がむちゃくちゃになりそう）