## 概要

[単振動を表す運動方程式](https://dic.okedou.app/words/p/zfOiTNBsI4m1c)、つまり

$$a=-\omega^2(x-x_0)$$

について考察する。加速度 $a$ は $x$ の2階の時間微分なので、

$$\frac{d^2x}{dt^2}=-\omega^2(x-x_0)\cdots\star$$

と表せる。

このように、$x$ のみが時間 $t$ の関数であり、$x$ の2階の時間微分も含む方程式を、**2階微分方程式**という。この方程式を満たす関数 $x$ を、微分方程式の**解**という。

全ての解を網羅した解の形を**一般解**というが、単振動の運動方程式 ($\star$) は、実は一般解を求めることができて、一般解は、任意の定数 $A,B$ を用いて、

$$x-x_0=A\sin\omega t+B\cos\omega t$$

で表される。[三角関数の合成](https://dic.okedou.app/words/p/svngexyQZEkIZ)を行うと、

$$x-x_0=A'\sin(\omega t+\theta_0)$$

で表すこともできる（$\theta_0$ は**初期位相**という）。つまり、**単振動をする物体の運動が、これで完璧に時間追跡できる**。

この一般解の考え方は、知らないと解けない問題は出てこないが、**数学が得意な方**は、知っていると単振動の式での理解がすごくしやすくなるのでオススメ。という程度の知識。

動画で例題と共に学びたい方は、[東大物理学科卒ひぐまさんの動画](https://okedou.app/videos/l445Z-t73pQ)がオススメ。

この式で運動方程式の全ての解が尽くされているという証明は、大学でしっかり学ぶとして、ここでは**この一般解が運動方程式 ($\star$) を満たすこと**を確認しよう。一般解を2階微分していくと、

$$
\begin{align}
\frac{dx}{dt}&=A\omega\cos\omega t-B\omega\sin\omega t\\\\
\frac{d^2x}{dt^2}&=-A\omega^2\sin\omega t-B\omega^2\cos\omega t\\\\
&=-\omega^2(x-x_0)
\end{align}
$$

となるので、運動方程式 ($\star$) を満たすことがわかる。

**定数 $A,B$ については、初期条件（$t=0$ のときの $x$、$v$ の値）によって定める。** 下の例で確認しよう。

## 使い方の例

一端が固定されたばね定数 $k$ の鉛直なばねの他端に、質量 $m$ の小球を付ける。ばねの自然長の位置を原点として、鉛直下向きに $x$ 軸をとる。

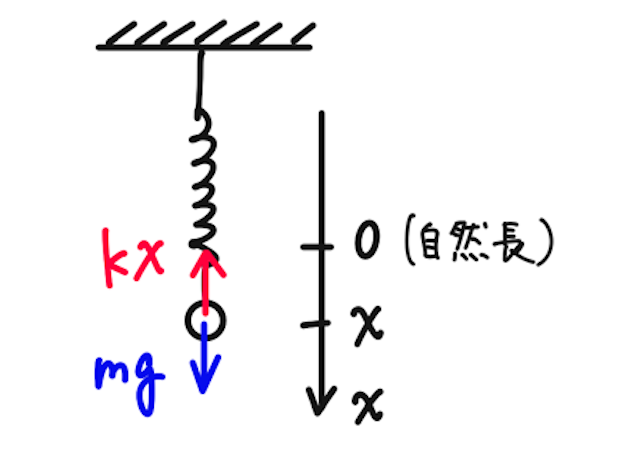
![Untitled 1 P1 133.png](https://oke-files.s3.amazonaws.com/uploads/EOhd9b0IYZ6GB/89c1afe982054b06a21c36b27837f729.png)

【例1】自然長の位置で静かに小球を離したとき、小球の変位の式を求めよ。

【解1】[運動方程式](https://dic.okedou.app/words/p/xskT5G8paROk7)は、

$$
\begin{align}
ma&=mg-kx\\\\
a&=g-\frac{k}{m}x\\\\
&=-\frac{k}{m}\left(x-\frac{mg}{k}\right)
\end{align}
$$

となるので、角振動数 $\omega=\sqrt{\displaystyle\frac{k}{m}}$ の単振動となる。一般解は、定数 $A,B$ を用いて、

$$x-\frac{mg}{k}=A\sin\sqrt{\displaystyle\frac{k}{m}} t+B\cos\sqrt{\displaystyle\frac{k}{m}} t$$

と求められる。**初期条件①として、$t=0$ のとき $x=0$** なので、上の一般解で $t=0$ を考えると、

$$-\frac{mg}{k}=B$$

を得る。さらに、一般解を一階微分して、速度 $v$ を求めると、

$$v=A\sqrt{\displaystyle\frac{k}{m}}\cos\sqrt{\displaystyle\frac{k}{m}} t-B\sqrt{\displaystyle\frac{k}{m}}\sin\sqrt{\displaystyle\frac{k}{m}} t$$

となる。**初期条件②として、$t=0$ のとき $v=0$** なので、

$$0=A\sqrt{\displaystyle\frac{k}{m}}$$

を得る。以上より、

$$A=0, \ B=-\frac{mg}{k}$$

なので、一般解は

$$x=\frac{mg}{k}-\frac{mg}{k}\cos\sqrt{\displaystyle\frac{k}{m}} t$$

となる。

【例2】自然長の位置で下向きに速さ $v_0$ を与えて小球を離したとき、小球の変位の式を求めよ。

【解2】[運動方程式](https://dic.okedou.app/words/p/xskT5G8paROk7)は、

$$
\begin{align}
ma&=mg-kx\\\\
a&=g-\frac{k}{m}x\\\\
&=-\frac{k}{m}\left(x-\frac{mg}{k}\right)
\end{align}
$$

となるので、角振動数 $\omega=\sqrt{\displaystyle\frac{k}{m}}$ の単振動となる。一般解は、定数 $A,B$ を用いて、

$$x-\frac{mg}{k}=A\sin\sqrt{\displaystyle\frac{k}{m}} t+B\cos\sqrt{\displaystyle\frac{k}{m}} t$$

と求められる。**初期条件①として、$t=0$ のとき $x=0$** なので、上の一般解で $t=0$ を考えると、

$$-\frac{mg}{k}=B$$

を得る。さらに、一般解を一階微分して、速度 $v$ を求めると、

$$v=A\sqrt{\displaystyle\frac{k}{m}}\cos\sqrt{\displaystyle\frac{k}{m}} t-B\sqrt{\displaystyle\frac{k}{m}}\sin\sqrt{\displaystyle\frac{k}{m}} t$$

となる。**初期条件②として、$t=0$ のとき $v=v_0$** なので、

$$
\begin{align}
v_0&=A\sqrt{\displaystyle\frac{k}{m}}\\\\
A&=v_0\sqrt{\displaystyle\frac{m}{k}}
\end{align}
$$

を得る。以上より、

$$A=v_0\sqrt{\displaystyle\frac{m}{k}}, \ B=-\frac{mg}{k}$$

なので、一般解は

$$x=\frac{mg}{k}+v_0\sqrt{\displaystyle\frac{m}{k}}\sin\sqrt{\displaystyle\frac{k}{m}} t-\frac{mg}{k}\cos\sqrt{\displaystyle\frac{k}{m}} t$$

となる。



単振動の一般解

概要

使い方の例

タグ