単位ベクトル

概要

単位ベクトルとは、 大きさが （つまり長さが ） のベクトルのこと。

零ベクトルでは無い、とあるベクトル が与えられた時に、そのベクトルの大きさで割ると、 同じ方向を向いた単位ベクトルが求められる、というのは、知っておくと結構便利なことがある。式で書くとこんな感じ。

大事なのは、

• 分母は、単なる値であること
• を、 以上の値で割っている、つまり、ベクトルを伸縮させているだけ（なので、同じ方向を向く）
• 自分自身の長さで割るので、必ず大きさが になる。（例えば大きさ のベクトルを で割ったら、大きさが のベクトルが出てくる）

というのをイメージで理解しておくこと。

絵で書くとこんな感じ。

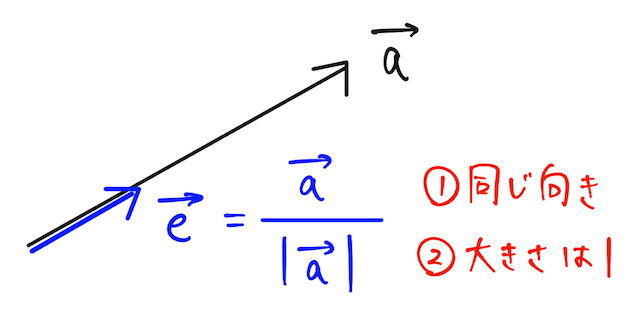
例

と同じ向きの単位ベクトルを求める。ベクトルの大きさは

なので、単位ベクトルは、

と求められる。

補足

やや発展的ではあるが、 正射影ベクトルを考える時にも大事になる、縁の下の力持ち的な概念。

また、 あるベクトルを 軸成分と 軸成分に分解するような使い方もする（もちろん空間でもOKだが、ここでは平面で話を進める）。つまり、 軸正の方向の単位ベクトルを 、 軸正の方向の単位ベクトルを とおくと、あるベクトル は、

として、 成分と単位ベクトルを使って表現することができる。これは、ベクトルの足し算を考えたら納得できると思う。

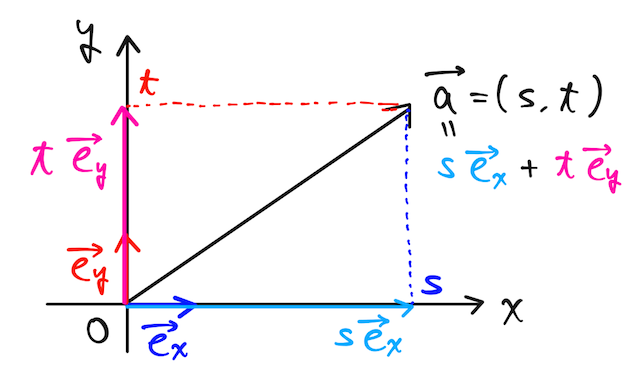
※成分が正のときで書いているが、負でも同様。

もしくは、成分で計算しても理解できると思う。つまり、、 なので、

こういう分解は、なかなか高校数学では登場してこないが、大学数学になると、鬼のように登場する。