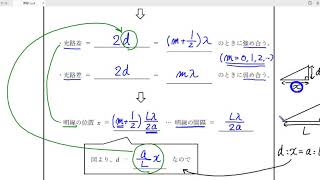
ニュートンリング

概要

大きな半径の球面（の一部）をもつ平凸レンズ（片方が平らで、もう片方が凸のレンズ）を、板ガラスの上に乗せて、上から波長 の単色光を入射させ、上から見ると、平凸レンズの下面で反射した光と、板レンズの上面で反射した光が干渉し、同心円上の縞模様が見える。これをニュートンリングという。

干渉実験シリーズの中でも、一番かっこいい名前をしていることでも有名。

実際に見てみると、ほんとにスキマ空いてるの？というくらいレンズ間は狭い。

このとき、その光の干渉条件は、 として、

となる。ただし、 は上のレンズの凸部分の球面半径、 は平凸レンズの中心軸からの距離を表す。

他の干渉実験では、「明線・暗線」と呼んでいたが、ニュートンリンクでは、その形状から、同心円上の縞模様ができるので、明線・暗線とはあまり言わない。

導出

こういう干渉の条件の導出はワンパターンなので、考え方を身につけてしまおう。

1. 光路差を考える

2. 位相のずれに注意する

3. 光路差が の整数倍か、整数 倍かで強め合い・弱め合いを判断する

光路差

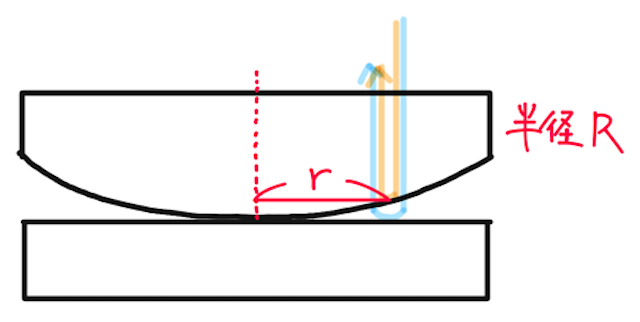
平凸レンズの中心軸から距離 の位置での、レンズ間の距離を とする。

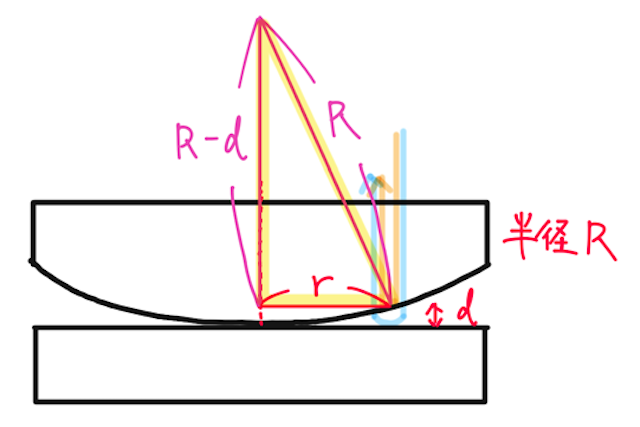
このとき、光路差（光路長の差、今回は空気中で考えているので距離の差でOK）は、往復分を考えて、

となる。では を や で表していこう。上の図の黄色の直角三角形について、三平方の定理より

ここで、 に比べて、十分に大きい球面半径 を考えているとすると、 の項は無視できるので、

と近似できるので、光路差は となる。

位相のずれ

干渉の問題で大事な事実として、

• 絶対屈折率が小さい媒質から、大きい媒質に入射する波が反射すると、位相が ずれる。
• 絶対屈折率が小さい媒質から、大きい媒質に入射する波が反射すると、位相はずれない。

正弦波の式を思い出すと分かる通り、位相が ずれるとは、中身の角度が ずれること。例えば、山で入射した波は谷として反射する。

この証明は大学になってから学ぶ事になるが、固定端・自由端と同じイメージで、硬そうなものにバンっとぶつかって反射するときには ずれて、柔らかそうなものにフニャっとぶつかって反射するときには位相はずれない、という理解をしておこう。

では、このニュートンリングの設定では、どこで位相がずれるだろうか。

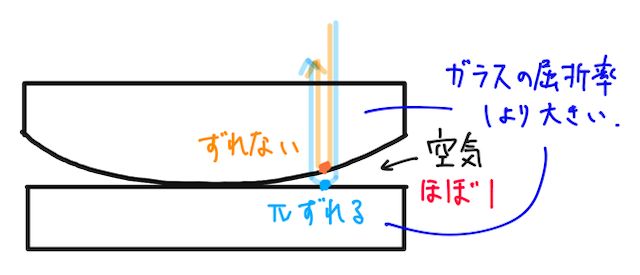
ガラスの絶対屈折率は、空気の絶対屈折率（ほぼ1）よりも大きいので、水色の波は、反射する際に位相が ずれるが、オレンジの波は、位相がずれるタイミングはない。

明線・暗線の条件

つの波に位相のずれがない場合は、

• 光路差が空気中（真空中）の波長 の整数倍であれば、重なった波はピタリと波形が一致するので、波は強め合い、明るく見える。つまり明線になる。
• 一方で、光路差が空気中（真空中）の波長 の整数 倍であれば、重なった波は完全に打ち消しあうので、波は弱め合い、暗く見える。つまり暗線になる。

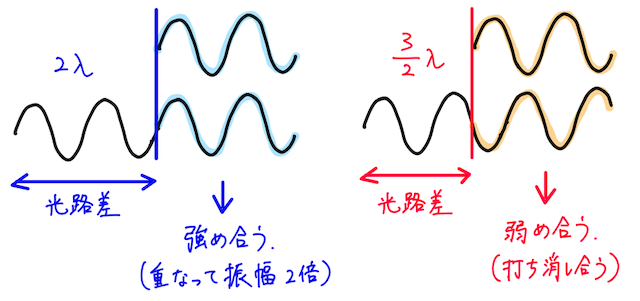
一方で、どこかで位相の のずれが起こっている場合には注意が必要で、強め合い、弱め合いの条件が逆になる可能性がある。今回のニュートンリングでは、水色の波だけ反射の際に ずれているので、

• 光路差が空気中（真空中）の波長 の整数倍のとき、位相のずれを考えると、重なった波は完全に打ち消しあうので、波は弱め合い、暗く見える。つまり暗線になる。
• 一方で、光路差が空気中（真空中）の波長 の整数 倍のとき、位相のずれも考えて、重なった波はピタリと波形が一致するので、波は強め合い、明るく見える。つまり明線になる。

よって、干渉の条件（明線・暗線の条件）は、 として、

であることが示される。

補足

問題によっては、明るいリングの半径 について考察することがある。

まずは、明るいリング（明るい円）となる条件を、 について整理すると、

となり、 のグラフの形状から、 が大きくなるにつれて、リングの間隔 は小さくなる。

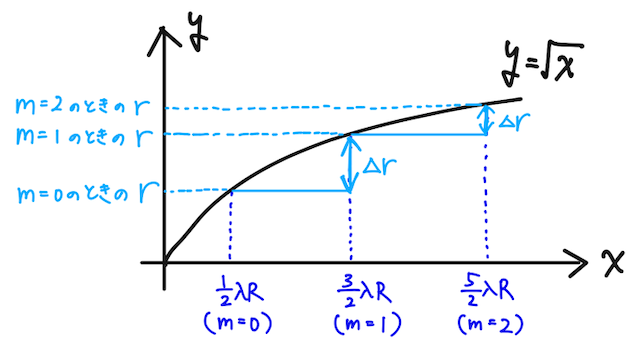
もっと式で示したい！という理系の方は、少し一般化して、

を考えて、導関数を求めると

となるので、 は単調減少、つまり差が縮まっていくことがわかる。

また、上のガラス板の上面や、下のガラス板の下面での反射波は考えなくていいのかと気になる人もいるかもしれないが、光路差が大きいため干渉縞は観測されない。つまり、光路差が大きくなると、その分干渉条件から も大きくなるが、 と の比が近づいていくので、波長が少しゆらぐと明線・暗線の条件が安定しなくなり、干渉縞の観測が厳しくなる。