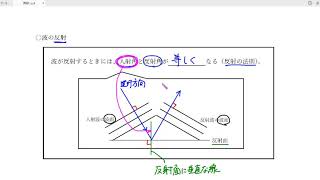
ホイヘンスの原理

概要

「波面上の各点からは、その点を波源とした球面波（素元波）が生じており、これらの球面波に共通に接する面（包絡面）が新たな波面になり、波が進む」

これをホイヘンスの原理といい、波の反射、屈折、回折などの重要な現象が説明できるようになるので、とても大事な原理。

日本語を解読しながら、どういうことを言っているのかイメージで確認しよう。

波面

波は基本的に 次元の空間内を伝わる。ある時刻において、位相の等しい点を連続的につないだ面のことを、波面という。例えば、山なら山同士を結んでいくようなイメージ。

特に、波面が平面になるような波を平面波、波面が球面になるような波を球面波という。

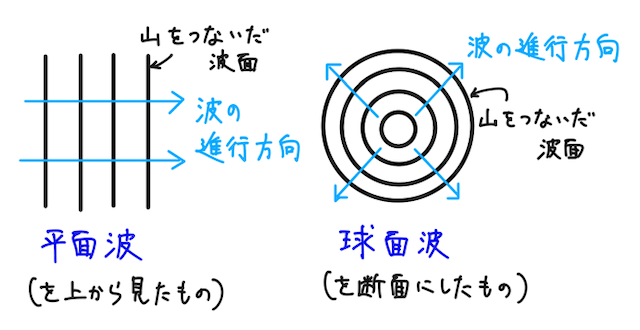
※ここではイメージとして、山をつないだ波面を考えたが、どの位相同士とつないで行っても良いので、波面はもっと無数にぎっしり詰まっている。

波面に垂直な直線を射線といい、波の進行方向は、射線の向き、つまり波面に垂直な向きとなる。

ホイヘンスの原理

直線状（1次元）の媒質を伝わる波の方向は、前か後ろなのでわかりやすいが、水面や空中（2次元、3次元）になると、波の方向や波面の形についてはなかなか考えにくい。

1678年にホイヘンスは、波が伝わっているときの波面の決まっていき方について、ある瞬間における波面上の各点が、新しい波源となって、各波源から球面波（素元波）が生じ、これらの素元波に共通に接する面が次の瞬間の波面となるという原理を提唱した。

絵で理解しておこう。

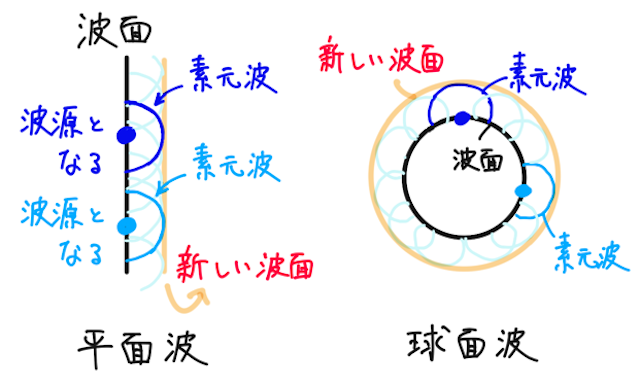
このホイヘンスの原理で説明できる法則として、

• 反射の法則
• 屈折の法則

などがあるので、合わせて理解しておこう。