相互誘導

概要

自己誘導と並んで、電磁気の最後の方に出てきて無視されがちな相互誘導だが、「なぜそんな現象が起こるのか」「どうやって公式が出てくるのか」がわかればとても面白い現象だとわかり、忘れなくなる。あと、補足で細かい話もしているので、そちらも是非。

まず自己誘導ってなんだっけ？という方は先に自己誘導の辞書で学習しよう。

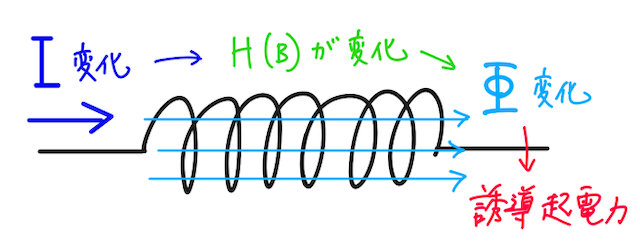
簡潔に言うと自己誘導とは、コイルを含んだ回路を考えたとき、コイルに流れる電流が時間によって変化すると、電流によって作られる磁場の強さも変化し、コイルを貫く磁束が時間によって変化することで、電磁誘導が生じて、変化を打ち消す方向にコイルに誘導起電力が生じる現象であった。

ここで、2つのコイルA, Bを考える（相互誘導は登場人物が2人になる）。コイルAには電源をつなぎ、電流を流す。しかしもう1つのコイルBとは同じ導線ではつながず、代わりに同じ鉄心に取り付けることにする。

1. この状態でコイルAに流れる電流が時間によって変化すると、
2. コイルAの自己誘導によって、鉄心を貫く磁束が時間によって変化することになる。
3. すると、同じ鉄心に巻かれているコイルBを貫く磁束が変化することになり、
4. それによりコイルBで電磁誘導が引き起こされ、誘導起電力が発生する。（コイルBに豆電球をつなぐと、ちゃんと光る）

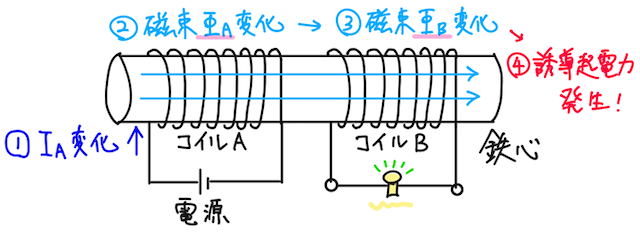
この現象が相互誘導である。つまり、コイルA, Bは同じ導線でつながっていないのに、離れたコイルに起電力を発生させることができる！

現象の理解はこれくらいにして、これを数式で表してみよう。

まずコイルAについて、電流の変化によって発生するコイルを貫く磁束 は、電流 に比例する（証明は自己誘導の辞書で）。そして、ここでは鉄心でつないでおり、コイルAとコイルBの間で磁束の漏れがないとすると、磁束 は全てコイルBも貫くので、コイルBを貫く磁束 も電流 に比例する。

そこで、この比例係数を とおくと、

と表せる。

これより、時間 の間に電流が 変化するとき、磁束の変化 は、

と表せる。よって、巻き数 のコイルBに生じる誘導起電力 は、ファラデーの電磁誘導の法則より、

を得る。ここで、比例係数をまとめて とおくと、

と表せる。この、相互誘導によって生じた起電力を、素直なネーミングで相互誘導起電力といい、この比例係数 のことを、相互インダクタンスと呼び、相互誘導の大きさを表す。単位は自己インダクタンスと同じくヘンリー を用いる。

この式は符号付きになっていて、レンツの法則 に従い、磁場の変化を打ち消す方向に誘導起電力がはたらくことを意味している。（自己誘導起電力では、電流の流れる向きをもとに向きを定めたが、相互誘導起電力では、コイルBに電流が流れているとも限らず、なかなか電流の向きで定義しづらい。細かいけれど）

補足

鉄心ってなんのためにあるのだろう？結局磁束が別のコイルに入っていくなら鉄心なくて良いんじゃない？むしろ勉強する鉄の心が欲しいわ、と思う方もいるかもしれない。実は鉄心を使うことで、

1. 透磁率を上げることができる
2. 磁束を閉じ込めておくことができる

といった良いことがある。詳しくいうと、

1.については、透磁率 が大きい方が、磁束密度 が大きくなり、磁束 が大きくなり、起電力 が大きくなる。

2.については、同じ鉄心で2つのコイルをつないでしまうことで、コイルAで発生した磁束を漏らさずにコイルBに送り込むことができるので、磁束 が大きくなり、起電力 が大きくなる。なので、別々の鉄心に巻き付けず、同じ鉄心に2つのコイルを巻き付ける。

ちなみに相互誘導は、変圧器に使われている技術として有名。海外旅行の際に、例えば日本のお気に入りのドライヤーを持っていくとすると、国によってコンセントの対応電圧が違うので、電圧を変えられる「変圧器」というプラグみたいなものを一緒に持っていくことになる。上で見たように、相互誘導の原理で別の回路に別の値の起電力を発生させることができるので、電圧の変換器の技術としてもってこいなのである。