回転座標系の運動方程式

概要

慣性の法則が成り立つ座標系である慣性系に対して、加速度 で並進運動をする加速度系で物体の運動を考察したとき、慣性力 が生じるとして考えれば良いことを、慣性力の辞書で学んだ。

では、慣性系に対して回転移動している座標系（回転座標系） から物体の運動を考察した場合、どのような慣性力がはたらくのだろうか。そりゃ遠心力でしょ、と思う方も多いかもしれないが、実はもう一つ慣性力が存在する。それを、回転座標系の運動方程式を立てることで調べよう。

ここではとりあえず2次元の運動を考えるが、3次元でも同様に考えることができる（大学で学ぶ）。

原点 を一致させ、慣性系 の原点の周りで一定の角速度 で反時計回りに回転している回転座標系 をとる。

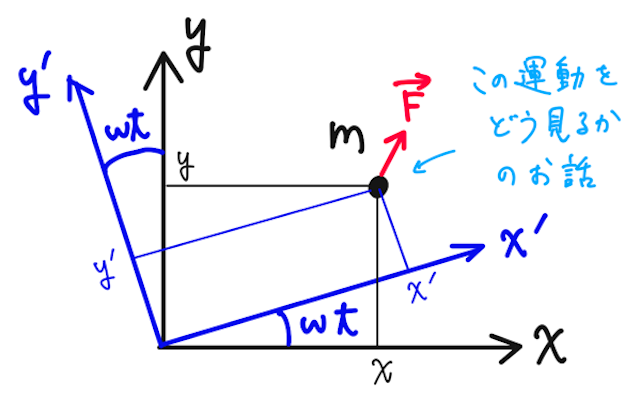
慣性系で、質量 の質点に力 がはたらいているとすると、慣性系での運動方程式は、

で表される。（ドットは見たことない方も多いと思うが、画面の汚れや折れたシャー芯ではなく、時間微分を表す。2つ付いていたら時間での2階微分。）

このとき、回転座標系 で記述した質点の運動方程式は、力の成分を とすると、

と表せる。この式の証明は、ややこしいので動画で学ぶことをオススメする。CSS高校物理さんの動画や、ヨビノリさんの動画（ベクトルのまま証明されていて、やや発展的）がオススメ。

ここでは、この運動方程式の形を理解することが大事で、これは、真の力 以外に、見かけの力である慣性力として、遠心力とコリオリ力というものが存在し、それぞれ成分は

• 遠心力
• コリオリ力

で表されることを意味している。（よくコリコリ力と書いてしまうので、気をつけよう）

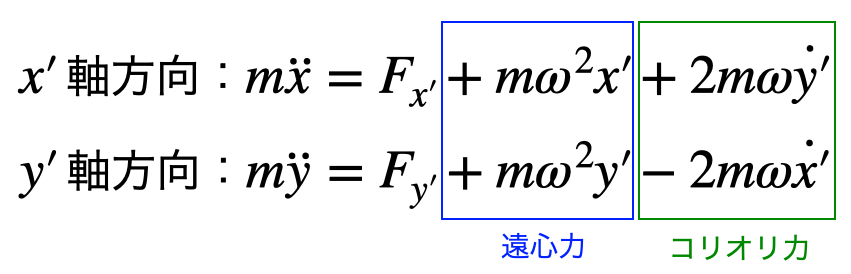
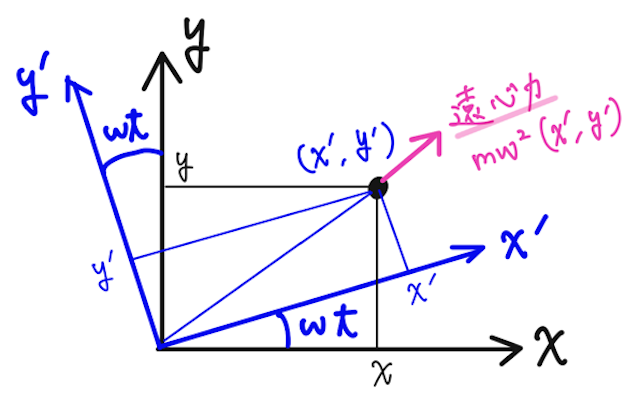
また、力の向きも大切で、遠心力は、

と表されるので、遠心力の向きは回転座標系の位置ベクトル と平行であり、回転中心から離れる方向にはたらくことがわかる。（例えば、 のところに位置していたら、力の 成分はプラスになるので、 軸正の向きに加速度を生じさせる）

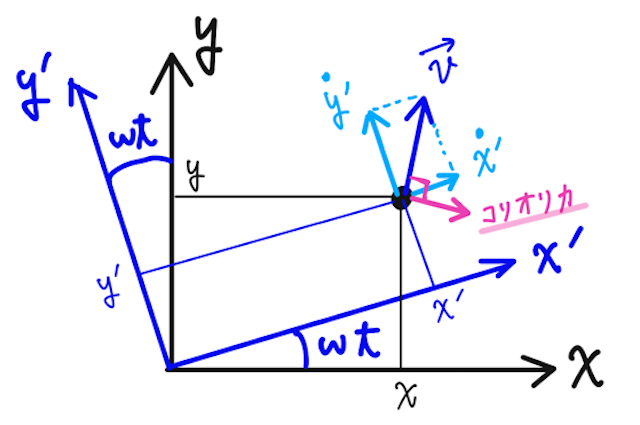
また、コリオリ力は、

であることから、力の向きは回転座標系での質点の速度に垂直で、進行方向に向かって右向きにはたらくことがわかる。（例えば、 成分も 成分もプラスの速度だった場合、力の 成分はプラス、 成分はマイナスになる）

等速円運動との関係

質点が、半径 、角速度 で等速円運動しているとき、角速度 で回転する回転座標系 でこの運動を考察する（常に とする）と、質点の速度は であるから、コリオリ力ははたらかず、運動方程式は、

となるので、真の力以外に、見かけの力として遠心力 のみ考えればいいことになる。これで遠心力の辞書で学んだ知識と一致するので、安心して夜眠ることができる。