概要
「分体積」とは、混合気体の成分が体積を分け合っていると仮想的に考える方法のこと。たとえば2種類の気体A・Bが体積の容器に混ざっているなら、本当はAもBもの空間を飛び回っているはずだけど、気体の計算のために気体が"住み分け"していると考える方法です。
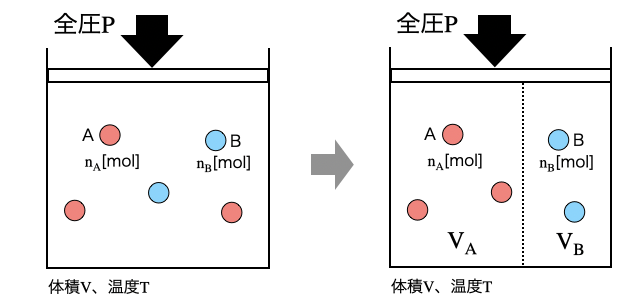
このとき、気体全体で圧力Pであると考えると、分体積の合計が体積になり、各分体積は(モル分率)×(体積)で求まります。
分圧と分体積とでは考える土俵が違うので、両方同時に使うことはないことに注意。
詳細
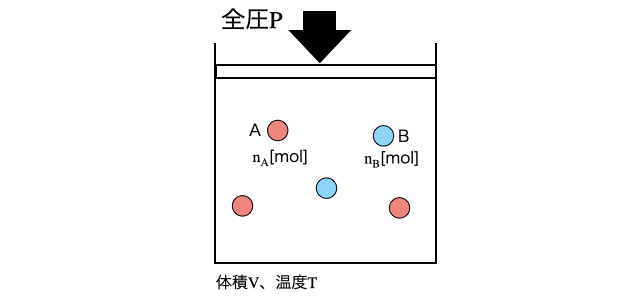
分体積では、空間を分割して混合気体の各成分が飛んでいるかのように考えます。このとき、[mol]のAが部分の圧力を担当し、[mol]のBが部分の圧力を担当すると考えると、数式の上でも辻褄があいます。
$であることを使えば、両辺を足して、
これは全体の状態方程式と一致しています。また(1つ目の式)÷(3つ目の式)、(2つ目の式)÷(3つ目の式)より、
です。
補足
- 混合気体を考えるのに、混合気体であれ各成分が飛び回る体積は同じと考えて圧力を分割したのが「分圧」、混合気体全体の圧力は等しいと考えて体積を分割したのが「分体積」です。つまり、体積一定で見るか圧力一定で見るか、見方が違うので2つの考え方を同時に使うことはありませんし、原則、現象に基づいている分圧だけ使えば全ての問題は解けます。
ただし、圧力一定で見る分体積は、例えば常に全圧が一定になるような問題などで便利に使える場合もあるので、余裕があれば知っておくとちょっとしたテクニックとしていいでしょう。詳しくは受験メモ山本の動画などをチェック!








