はみだしけずり論法
概要
数学3の面積の問題を解いていると、下のような、曲線と直線で囲まれた部分(斜線部)の面積の最小値を求める場面に出くわすことがある。
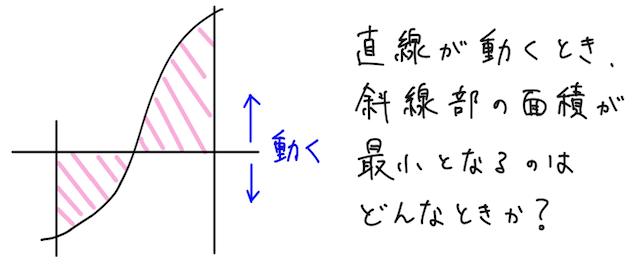
このような問題で、曲線が単調に増加したり減少したりする場合には、直線を動かして、面積の増減を視覚的に考えることで、面積の和が最小となる条件をラクに考えることができる。
結論としては下の図のように、線分の長さが等しくなるとき(★)に面積が最小となる。
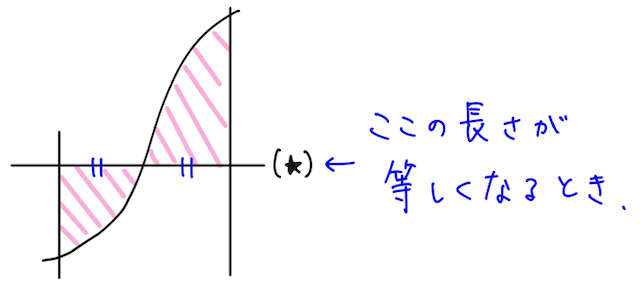
以下、理由を考えてみる。(関数は単調増加とする)
まず直線が(★)よりも上にある場合には、直線を下げると、減る部分(水色)の面積の方が、増える部分(黄緑)の面積よりも大きいので、面積の和を小さくできる。
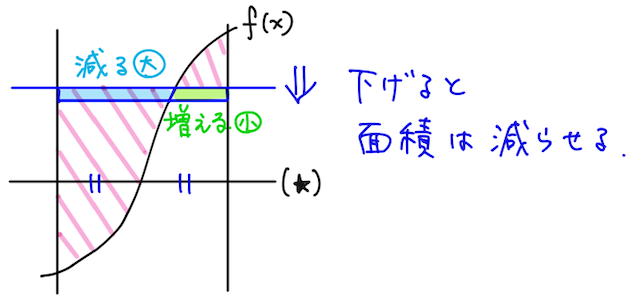
※ イメージとしては、減る部分(水色)と増える部分(黄緑)を長方形と見て面積を比較すると、高さが等しく横幅が水色の方が大きいので、直線を下げると面積の和が小さくなる感じ。
同様に、直線が(★)よりも下にある場合には、直線を上げると、減る部分(黄緑)の面積の方が、増える部分(水色)の面積よりも大きいので、面積の和を小さくできる。
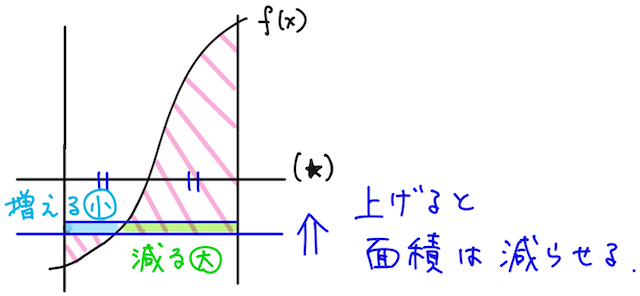
※ イメージとしては、減る部分(黄緑)と増える部分(水色)を長方形と見て面積を比較すると、高さが等しく横幅が黄緑の方が大きいので、直線を上げると面積の和が小さくなる感じ。
いずれにしても、どこまで面積の和を小さくできるかというと、減る部分と増える部分の面積が等しくなるときまで。
そのとき、減る部分と増える部分の横幅が等しくなるので、線分の長さが等しくなるとき(★)に面積が最小となることが納得できる。
このように、視覚的に面積が最小値となる状況を議論する方法を 「はみだしけずり論法」 という(大学への数学シリーズの用語)。ちょっと動かしてみて、面積の増減を考えるのがポイント!
受験で使っていいかどうかについては諸説あるが、教科書には出てこないようなので、答えの当たりをつけたり、検算として使ったりするのがオススメ。
例
例えば、
を最小にする
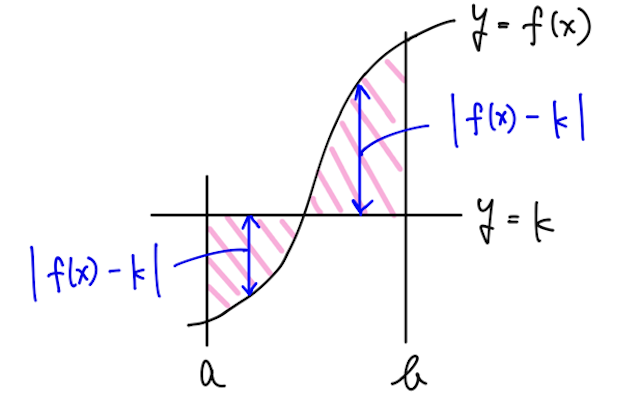
つまり、
それは、上の論法から
と求められる。
発展的な例
上のような形だけではなく、直線が斜めの場合にも威力を発揮することがあるので、例で考えてみる。
例えば単調増加で下に凸、かつ
が最小となる
上の例と同じように、この定積分を面積として捉えると、下の領域の面積の和を表すことになる。
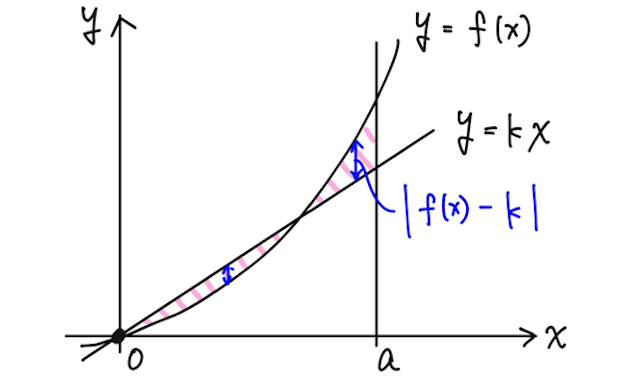
つまり、
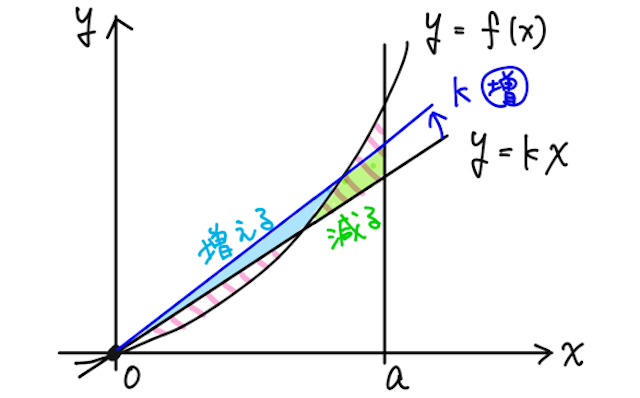
面積の和が最小となるのは、増える部分と減る部分の面積が等しくなるとき。つまり、下の面積
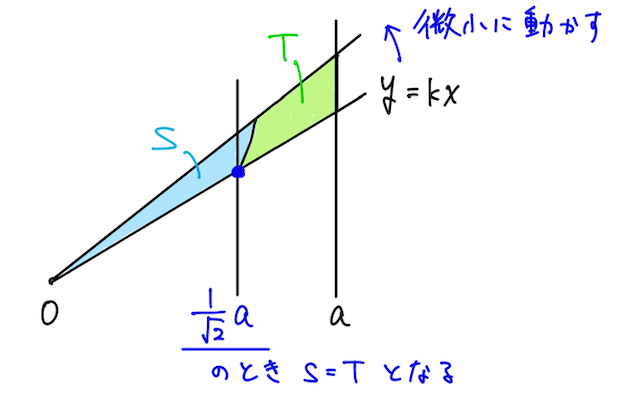
このとき、
となるので、それぞれの図形を三角形と見ると、その面積比が
よって、
と求められる。(最初の例では長方形と見て面積を比較したのと異なり、今回は片方が動かないので三角形と見て面積を比較する点に注意。)
補足
はみだしけずり論法が威力を発揮する問題として、北海道大学2022年理系第2問がある。
直接は使わないにせよ、はみだしけずり論法で見通しをつけないと時間がかかり過ぎてしまうため、知っておいても損はないと思われる。
ちなみに、「はみだしけずり」という命名については他に良い名前がありそうな気もするが、なかなか代案が思いつかないことで有名。
関連動画
関連用語




