正射影ベクトル

概要

を、 が定める直線に正射影したベクトルは、

で表される。上から光を当てて、 を が定める直線に投影したようなベクトルのこと。

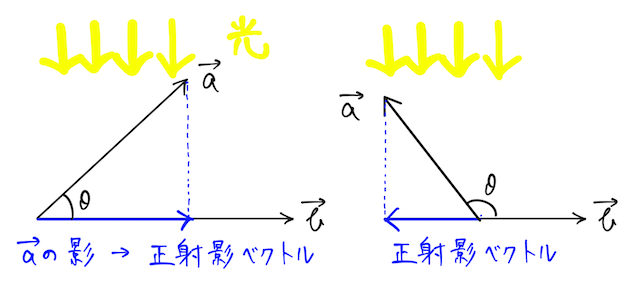
これは高校数学では発展的な事項であり、この式は覚えるよりも、下の図と導き方のイメージを理解して、作れるようになれれば十分。下の補足も確認しよう。

証明

と同じ向きの単位ベクトル は、

で求められる。ここで、 と の内積を考える。 つのベクトルのなす角を とおく。単位ベクトルの長さは なので、内積は

という値になり、これは、正射影ベクトルの符号付き長さとなっている（なす角が鈍角のときは負の値になる）。

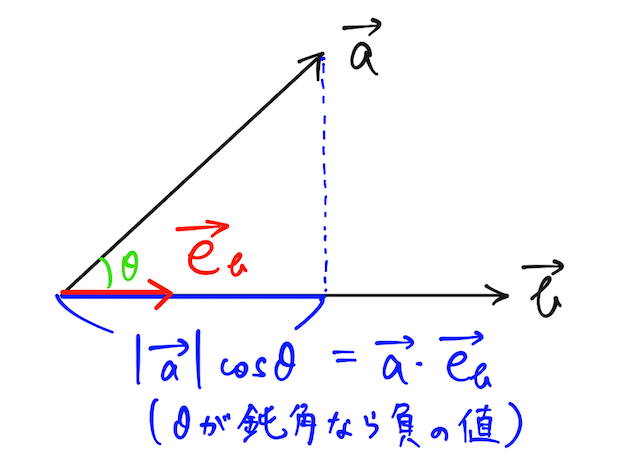
よって、この値を単位ベクトル をかけると、正射影ベクトルを求めることができ、

となって導かれる。

補足

や はベクトルではなく単なる値なので、この正射影ベクトルの式は、 という形になっていて、 と平行という認識が大事。

「で、何が嬉しいの？」と思う方も多いと思うが、難関大の問題や定理の証明などに、この概念がとても役に立つことがある。例えば、こちらのガチノビさんの点と直線の距離の導出動画がとても鮮やかで参考になるので見てみよう。（下の関連動画から、正射影ベクトルの入試問題への応用方法も学べる）