相関係数

概要

つのデータ にどれくらい関連性があるかを表す値の つを 「相関係数」 といい、

で求めることができる。「データの分析」分野のクライマックスということで、いろんな他の言葉も登場する。ディズニーランドのパレードのようなもの。

ここで、 の共分散は

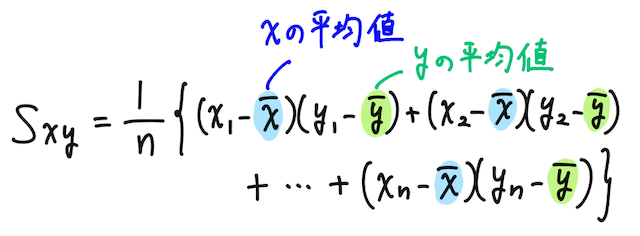
で求めることができ、 の標準偏差は以下の通り求められる。

これらを用いて、相関係数を計算することができる。

また、相関係数 については、 が成り立ち、相関との関係は、

• 相関係数 の値が に近いほど、 正の相関が強くなる。このとき、散布図は右上がりに分布する。
• 相関係数 の値が に近いほど、 負の相関が強くなる。このとき、散布図は右下がりに分布する。
• 相関係数 の値が に近いときは、相関は弱くなる。

例

例えば、 人の生徒の身長と体重を調べた結果が以下の通りだったとする。

身長（これを とする）の平均値は、

と計算できる。体重（これを とする）の平均値は、

と計算できる。よって共分散は、

と求められる。 の標準偏差はそれぞれ、

と計算できて、相関係数は、

となる。 人の身長と体重のデータには強い正の相関があることがわかる。

補足

相関係数には単位は無い。

相関係数は、英語で「correlation coefficient」という。「co」がそろっているので、口に出すと結構リズミカルな言葉になる。

実は、共分散や相関係数は、 やベクトルの内積とからめた面白いテーマ なので、なんでこんな形を考えるのか、興味がある方は、例えばぶおとこばってんの「データの分析のまるごと解説」の動画を見てみよう。

また、相関があるからといって、それは因果関係を表すわけではない点に注意しよう。これは、大学に入って研究をする際などに大事な認識となる。興味のある方は、例えばヨビノリさんの動画で学んでみよう。