ラジアン

概要

角度を、慣れ親しんだ 45° や 90° といった「°」（度）という単位（度数法）ではなく、 ラジアン（）という角度の単位を使って測ることを 弧度法（こどほう） という。名前は強そうだが、慣れてしまえば大したことはない。

「°」（度）という度数法では、円周を360等分した弧の、中心に対する角度を「1°」と定義していた。（1周が 360° であることを考えるとわかりやすい）

では、ラジアン（）はどうやって測る単位かというと、円の半径に等しい長さの弧の中心に対する角度を と定義し、弧の長さを半径の長さで割ったものを、その孤の中心角の角度 [] とするもの。

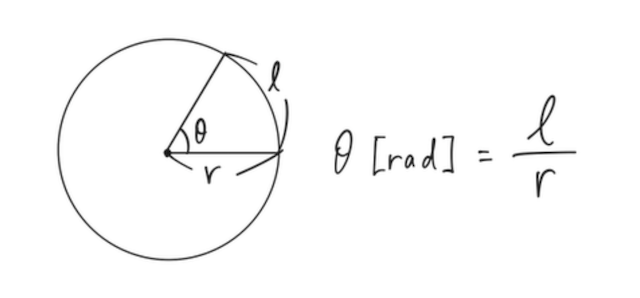
「°」（度）とラジアン（）の関係も大事で、中心角が や の孤を考えてみよう。中心が の円で考えると、定義から

• 中心角が のとき、孤の長さは となるので、ラジアンで測った中心角は
• 中心角が のとき、孤の長さは となるので、ラジアンで測った中心角は

つまり、

となる。これは絶対に理由も合わせて押さえておこう。

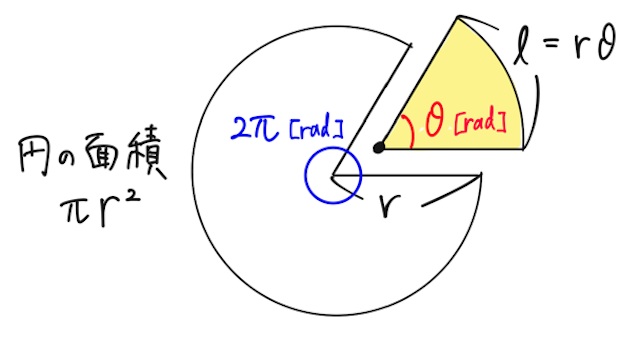
また、おうぎ形の半径を 、弧度法で測った中心角を とするとき、弧の長さ とおうぎ形の面積 は

と表せる。

上はラジアンの定義から納得できる。

下は、全体の円を中心角に比例して分割すると考えて

から出てくる。

補足

• ラジアンと弧度法の定義については、2018年のセンター試験で突如現れたことでも有名
• 三角関数などで、 角度に単位が示されていないときは、基本的にラジアンで測られていると考えると良い
• は くらい
• ちなみに、女性コンビで初めてM-1グランプリの決勝に進んだのは「アジアン」