概要
波の形が のような形になる波のことを、正弦波という。 を日本語に訳すと「正弦」なので、納得できるネーミングセンス。
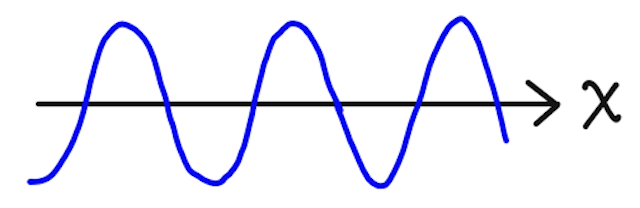
単振動をする波源から、 軸正の向きに、速さ で伝わる正弦波を考える。正弦波の振幅を 、周期を 、波長を とし、原点 にある波源の、時刻 での変位 が単振動の式
で表されるとする(つまり では変位が であることを仮定している)。これはどう解釈すれば良いかというと、 に具体的に値を代入するとわかるとおり、
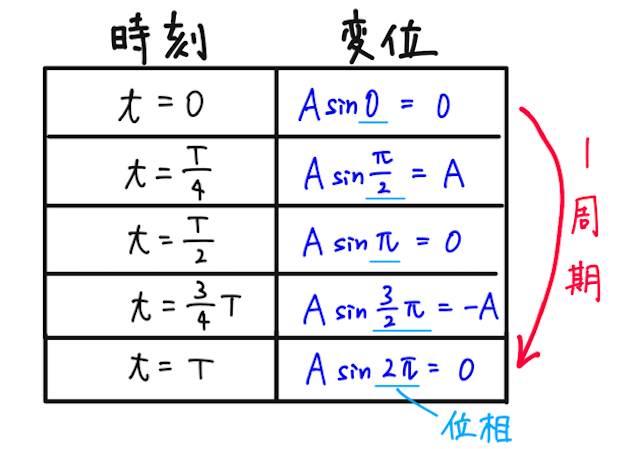
確かに のときに のときの状態に戻ってくる。つまり、 は周期が の正弦波を表しているということが納得できる。
ちなみに、正弦波を考える上で大事な用語として、位相というものがある。これは要するに の中身の角度のことで、媒質がどのような振動状態にあるかを表す。波の式が上で表されるとすると、位相は である。
話を戻して、原点 にある波源の、時刻 での変位 が () で表されるとき、位置 にある媒質 の、時刻 での変位 は、
で表される。これを正弦波の式、または波の式と呼ぶ。
これは覚えると脳のメモリを消費するので、省エネで行きたい方は導き出せるようにしておこう。
導出
考え方①(時刻 に注目)
まず、時刻 に注目して導出してみよう。
波が、原点 から位置 の点 まで到達する時間は、
であるので、いま求めようとしている時刻 のときの点 の媒質の変位は、時刻 での原点 での媒質の変位に等しい。(下の図の緑の線の通り)
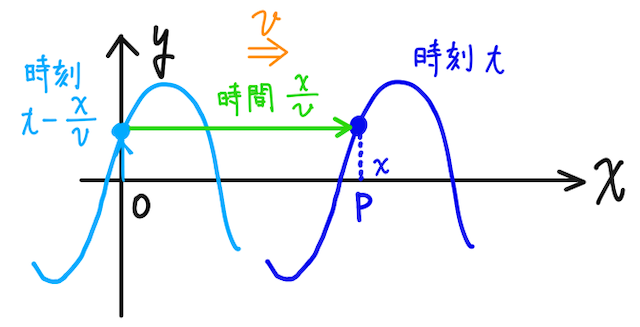
原点 での時刻 の変位は () で表される、つまり
であるので、同じ点での時刻 での媒質の変位は、
となる。よってこれが、求めるべき時刻 での点 の媒質の変位となる。もう少し変形をすると、波の基本式より
なので、これを代入して整理すると、
を得る。
考え方②(位置 に注目)
原点 での時刻 の変位が () で表されることから、下のような変位の グラフが描ける。
ここから、時刻 での グラフで考えでみよう。どのような波形になっているだろうか?
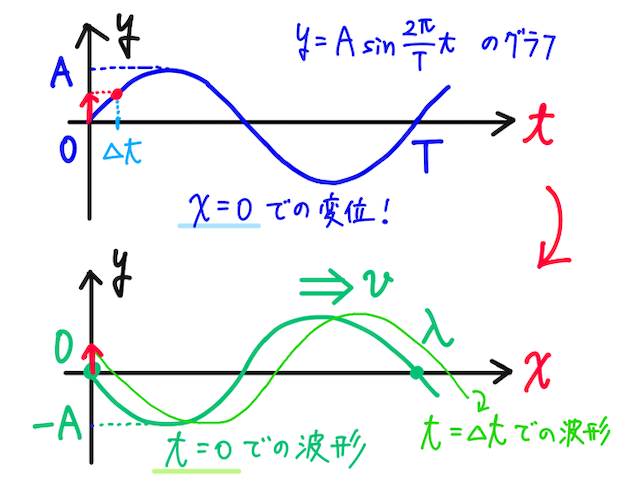
少し時間が経った時刻 での、原点 の変位を考えると、 での グラフは、上の緑の形になっていることが納得できる。
よって、時刻 での グラフの式は、
と表される。( から までが1周期となることを理解すれば、位相の形も納得できる!)
時刻 のときには、この波が 軸正の向きに だけ移動しているので、位置 にある点 の媒質の変位は、
ここで、波の基本式より
なので、これを代入して整理すると、
を得る。
使い方
この正弦波の式は一般に、変数として と登場してややこしいが、一文字固定することによって、 通りの見方ができるので、必ず押さえておこう。
- を止めて、時刻 と媒質の変位 の関係式と見れば、その位置での媒質の変位の時間変化の式、 グラフの式を表す
- を止めて、位置 と媒質の変位 の関係式と見れば、その時刻での波形の式、 グラフの式を表す
ことになる。例えば上の式で
- を代入すると、確かに原点での媒質の変位の式 () を表すことがわかる
- を代入すると、確かに時刻 での波形の式 () を表すことがわかる
補足
じゃあもう1個の を止めたらどうなるんだ!と感じた方は鋭くて、これについて少し考えてみよう。
を止めるということは、変位が同じ、すなわち位相が等しいという条件を で表すことになり、実はここから波の速度の情報が得られる。例えば上の式で、 をある値 で固定し、このとき位相が であるとする。つまり、
とする。この両辺を で微分すれば、
となり、波の速度が という結果が得られることになる。
また、今回は 軸正の向きに動く波を考えたが、負の向きに速さを持つ場合には、素直に を に変えれば正弦波の式は成り立つが、あまり出てこない。興味のある方は、上の導出と同様にして、理由を考えてみよう。










