Verifying Trigonometric Identities Pt 1
概要
動画投稿日|2011年12月8日
動画の長さ|13:41
Using the fundemental identities and the Pythagorean Identities, I go over multiple examples of verifying trigonometric identities.
It is very important in proofs that you do not handle it like an equation moving terms and factors from side to side.
I was corrected that what I am trying to prove should not be within the body of the proof. This implies it has already been assumed to be true. So proofs should be shown like this example:
cos^2(x)(tan^2(x)+1)=1
Proof:
cos^2(x)(tan^2(x)+1)=cos^2(x)*sec^2(x)
=cos^2(x)(1/cos^2(x))
=1
I reshot the intro with permanent corrections instead of just the annotations that are at the beginning of this video. • Verifying Trigonometric Identities Pt 1
Verifying Trigonometric Identities Part 2
• Verifying Trigonometric Identities Pt2
Verifying Trigonometric Identities Part 3
• Verifying Trigonometric Identities Pt3
Check out http://www.ProfRobBob.com/, there you will find my lessons organized by class/subject and then by topics within each class. Find free review test, useful notes and more at http://www.mathplane.com/ If you'd like to make a donation to support my efforts look for the "Tip the Teacher" button on my channel's homepage / profrobbob
関連動画
9:09
Verifying Trigonometric Identities Pt3ProfRobBob
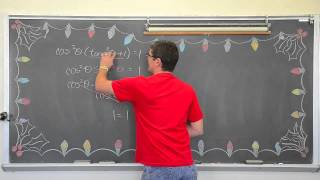
14:25
Verifying Trigonometric Identities Pt 1ProfRobBob

15:31
Verifying Trigonometric Identities Pt2ProfRobBob
14:25
Verifying Trigonometric Identities Involving Sum & DifferenceProfRobBob

17:35
Trigonometry Proofs Involving Half and Double AnglesProfRobBob
関連用語