整数の世界に虚数を一滴垂らす part2 ~素数が素数でなくなる世界~

オリンピックは男女バレーと錦織選手だけ欠かさず観戦しています。

おはこんばんは、ぱたです。


今回は「整数の世界に虚数を一滴垂らす」と題して、フェルマーの二平方和定理の証明の概要を3パートにわたってお送りしています。

この記事はpart2です！ part1はコチラ


※part2から内容的にはゴリゴリの大学数学です(笑)できるだけ専門用語を使わずに記事を書くようにしていますが、大学数学に興味のある方向けに一応専門用語や数学的背景を()で囲んで追記しています。雰囲気だけ掴みたい人は()を読み飛ばしてください！

復習：フェルマーの二平方和定理

まずは前回の記事の復習から。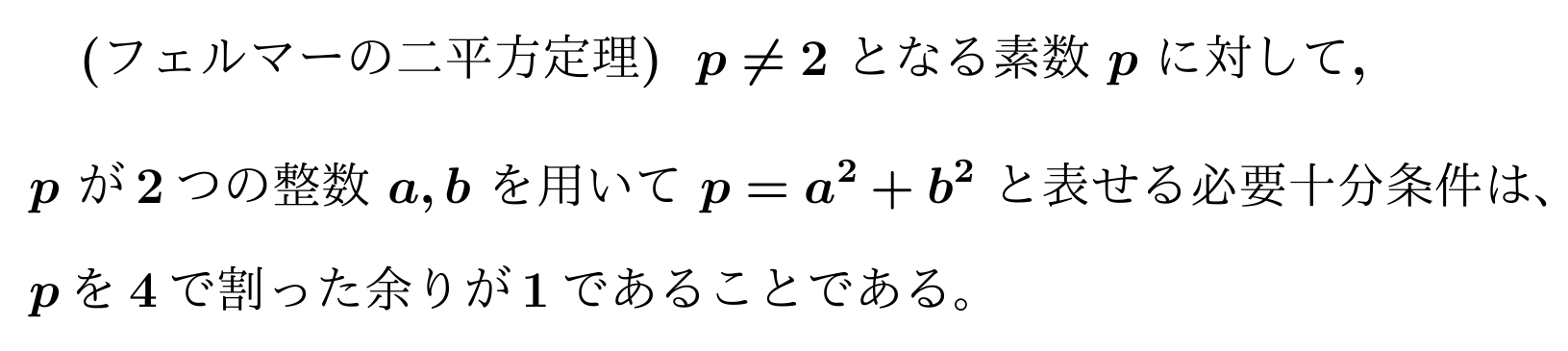



「p = a^2 + b^2 と表せる」⇒「pは4で割った余りが1である」は高校数学の範囲で証明することができます。

(平方数は4で割った余りが0か1しかあり得ないことを使えばよい)


しかし、「pは4で割った余りが1である」⇒「p = a^2 + b^2 と表せる」の証明は難しいです。


前回の記事の最後で議論した証明の方針を振り返りましょう。


高校数学では p = a^2 + b^2 のような整数問題は、因数分解をして解く方法が定石ですよね。


実は、この高校数学でも使われる発想が、証明の大きなカギとなるのです。


ただ、x^2+y^2 は因数分解できませんよね？でもそれは「整数の範囲」でのお話です。


しかし、整数の世界に虚数iを一滴垂らした世界の範囲では因数分解ができます。

証明の方針

ここら辺で「整数の世界に虚数iを一滴垂らした世界」というものを数学的にしっかり記述しておきましょう。




例えば 1+2i とか -7+3i は Z[i] の元です。


Z[i] の中では x^2+y^2 を以下のように因数分解することができます。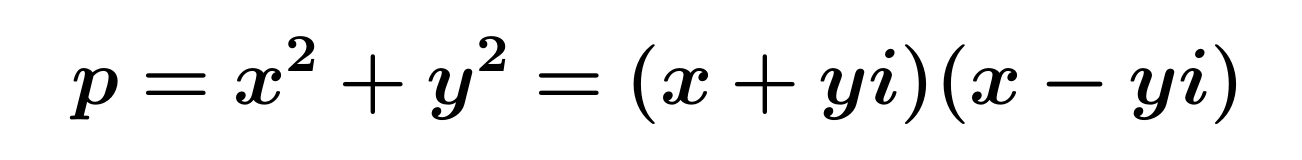





x,y は整数なので、x±yi は Z[i] の元です。


ここでひとつ疑問が生まれます。


「p って整数の世界では素数(厳密にはZの素元)だけど、Z[i] の世界でも素数(素元)なの？？」


もしすべての(Zの世界での)素数 p が Z[i] の世界でも素数なら、p は2つの Z[i] の元 α,β (厳密には単数でない Z[i] の元)の積 αβ と表すことはできません。とくに α = a+bi, β = a-bi とすれば、 p = (a+bi)(a-bi) = a^2+b^2 と表すことができないことが分かります。


でもフェルマーの二平方和定理は、 4で割った余りが1である素数 p は p = a^2 + b^2 と表すことができると主張しているわけです。


以上の考察から、


「pは4で割った余りが1である」⇒「p = a^2 + b^2 と表せる」を示すには


「4で割って1あまるような素数 p は、 Z[i] の世界では素数でない」ことを示せばよいということが分かります！


これを証明するためには、「ウィルソンの定理」という道具を使うのですが...


part2はここまで！


次回はこのウィルソンの定理を使ってフェルマーの二平方和定理の証明を結論付けることにしましょう。


最後に、「素数 p が Z[i] の世界で素数でない」という少し捉えにくい事実に具体例を与えておきます。


例えば p = 5 のとき、これは整数 Z の世界ではもちろん素数ですが、Z[i] の世界では 5 = (2+i)(2-i) と素因数分解することができるので素数ではありません。

このことから、 5が x^2 + y^2 という形で表せるかどうかは、5 が Z[i] の世界で素数であるかどうかに帰着されるわけです。


それでは次の記事でお会いしましょう、さようなら。